เกี่ยวกับตรีโกณมิติ

รูปสามเหลี่ยมสองรูปจะเรียกว่าคล้ายกัน ถ้ารูปหนึ่งสามารถขยายได้เป็นอีกรูปหนึ่ง และจะเป็นกรณีนี้ก็ต่อเมื่อมุมที่สมนัยกันมีขนาดเท่ากัน ตัวอย่างเช่น รูปสามเหลี่ยมสองรูปที่มีมุมร่วมกันมุมหนึ่ง และด้านที่ตรงข้ามกับมุมนั้นขนานกัน เป็นข้อเท็จจริงว่ารูปสามเหลี่ยมที่คล้ายกัน ด้านแต่ละด้านจะเป็นสัดส่วนกัน นั่นคือ ถ้าด้านที่ยาวที่สุดของรูปสามเหลี่ยมหนึ่ง ยาวเป็นสองเท่าของด้านที่ยาวที่สุดของรูปสามเหลี่ยมที่คล้ายกัน จะกล่าวได้ว่า ด้านที่สั้นที่สุดจะยาวเป็นสองเท่าของด้านที่สั้นที่สุดของอีกรูปสามเหลี่ยม และด้านที่ยาวปานกลางก็จะเป็นสองเท่าของอีกรูปสามเหลี่ยมเช่นกัน อัตราส่วนระหว่างด้านที่ยาวที่สุดและด้านที่สั้นที่สุดของรูปสามเหลี่ยมแรก จะเท่ากับ อัตราส่วนระหว่างด้านที่ยาวที่สุดและด้านที่สั้นที่สุดของรูปสามเหลี่ยมอีกรูปด้วย
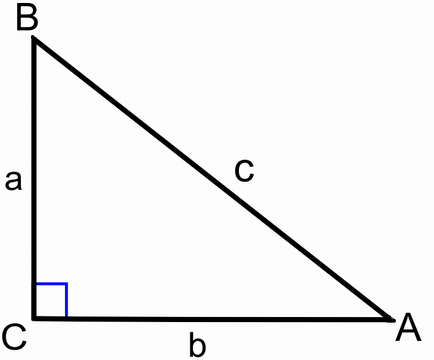
รูปสามเหลี่ยมมุมฉาก
จากข้อเท็จจริงเหล่านี้ เราจะนิยามฟังก์ชันตรีโกณมิติ เริ่มต้นด้วยรูปสามเหลี่ยมมุมฉาก ซึ่งเป็นรูปสามเหลี่ยมซึ่งมีมุมฉากหนึ่งมุม (90 องศา หรือ π/2 เรเดียน) ด้านที่ยาวที่สุดในรูปสามเหลี่ยมใดๆจะอยู่ตรงข้ามกับมุมที่ใหญ่ที่สุด แต่เพราะว่าผลรวมของมุมภายในรูปสามเหลี่ยมเท่ากับ 180 องศา หรือ π เรเดียน ดังนั้นมุมที่ใหญ่ที่สุดในรูปสามเหลี่ยมนี้คือมุมฉาก ด้านที่ยาวที่สุดในรูปสามเหลี่ยมจึงเป็นด้านที่ตรงข้ามกับมุมฉาก เรียกว่า ด้านตรงข้ามมุมฉาก
นำรูปสามเหลี่ยมมุมฉากมาสองรูปที่มีมุม A ร่วมกัน รูปสามเหลี่ยมทั้งสองนี้จะคล้ายกัน และอัตราส่วนของด้านตรงข้ามมุม A ต่อด้านตรงข้ามมุมฉาก จะเท่ากันทั้งสองรูป มันจะเป็นจำนวนระหว่าง 0 ถึง 1 ขึ้นอยู่กับขนาดของมุม A เท่านั้น เราเรียกว่า ไซน์ของ A และเขียนด้วย sin (A) ในทำนองเดียวกัน เรานิยาม โคไซน์ของ A คืออัตราส่วนระหว่าง ด้านประชิดมุม A ต่อด้านตรงข้ามมุมฉาก
\sin A = {\mbox{opp} (a) \over \mbox{hyp} (c) } \qquad \cos A = {\mbox{adj} (b) \over \mbox{hyp} (c) }
ฟังก์ชันเหล่านี้เป็นฟังก์ชันตรีโกณมิติที่สำคัญ ฟังก์ชันอื่นๆสามารถนิยามโดยใช้อัตราส่วนของด้านต่างๆของรูปสามเหลี่ยม แต่มันก็สามารถเขียนได้ในรูปของ ไซน์ และ โคไซน์ ฟังก์ชันเหล่านี้คือ แทนเจนต์, ซีแคนต์, โคแทนเจนต์, และ โคซีแคนต์
\tan A = {\sin A \over \cos A} = {\mbox{opp} (a) \over \mbox{adj} (b) } \qquad \sec A = {1 \over \cos A} = {\mbox{hyp} (c) \over \mbox{adj} (b) }
\cot A = {\cos A \over \sin A} = {\mbox{adj} (b) \over \mbox{opp} (a) } \qquad \csc A = {1 \over \sin A} = {\mbox{hyp} (c) \over \mbox{opp} (a) }

**NOTE : csc คือ cosec
วิธีจำ ไซน์ โคไซน์ แทนเจนต์ อย่างง่ายๆคือจำว่า ข้ามฉาก ชิดฉาก ข้ามชิด (ไซน์-ด้านตรงข้าม-ด้านตรงข้ามมุมฉาก โคไซน์-ด้านประชิด-ด้านตรงข้ามมุมฉาก แทนเจนต์-ด้านตรงข้าม-ด้านประชิด)
ที่ผ่านมา ฟังก์ชันตรีโกณมิติถูกนิยามขึ้นสำหรับมุมระหว่าง 0 ถึง 90 องศา (0 ถึง π/2 เรเดียน) เท่านั้น หากใช้วงกลมหนึ่งหน่วย จะขยายได้เป็นจำนวนบวกและจำนวนลบทั้งหมด (ดูใน ฟังก์ชันตรีโกณมิติ)
ครั้งหนึ่ง ฟังก์ชันไซน์และโคไซน์ถูกจัดลงในตาราง (หรือคำนวณด้วยเครื่องคิดเลข) ทำให้ตอบคำถามทั้งหมดเกี่ยวกับรูปสามเหลี่ยมใดๆได้อย่างแท้จริง โดยใช้กฎไซน์ และ กฎโคไซน์
กฎเหล่านี้สามาถใช้ในการคำนวณมุมที่เหลือและด้านของรูปสามเหลี่ยมได้ เมื่อรู้ความยาวด้านสองด้านและขนาดของมุมหนึ่งมุม หรือรู้ขนาดของมุมสองมุมและความยาวของด้านหนึ่งด้าน หรือ รู้ความยาวของด้านทั้งสามด้าน
นักคณิตศาสตร์บางคนเชื่อว่าตรีโกณมิติแต่เดิมนั้น ถูกประดิษฐ์ชึ้นเพื่อใช้คำนวณนาฬิกาแดด ซึ่งมักเป็นโจทย์ในหนังสือเก่าๆ มันมีความสำคัญมากในเรื่องการสำรวจ
ความสัมพันธ์ของอัตราสวนตรีโกณมิติ 
 sin A . cosec A = 1
 cos A . sec A = 1
 tan A . cot A = 1
 tan A =  cosA หารด้วย sinA
 cot A = sinA หารด้วย  cosA
 cos ยกกำลังสอง A+sin ยกกำลังสอง A = 1
 sec ยกกำลังสอง A - tan ยกกำลังสอง A  = 1 
 cosec ยกกำลังสอง A - cot ยกกำลังสอง A = 1

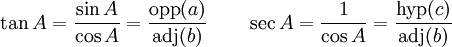
ไม่มีความคิดเห็น:

แสดงความคิดเห็น

สมัครสมาชิก: บทความ (Atom)